
Se pueden encontrar ejemplos de la proporción áurea en todas partes en la arquitectura clásica, las obras de arte, la naturaleza e incluso la música. Esta expresión de proporción, también conocida como la Proporción Divina, ofrece una composición armoniosa a través de la aplicación de un número irracional (1,618) en el diseño, tanto natural como humano. Lo más probable es que desconozca las matemáticas detrás de la belleza de la proporción áurea porque produce objetos y música que naturalmente le agradarán sin necesidad de ninguna explicación.
Proporción áurea en arquitectura
La proporción áurea crea una belleza casi perfecta en la naturaleza y el arte. Cuando comience a buscar ejemplos de la proporción áurea en la vida cotidiana, es posible que se sorprenda de los muchos casos en que se ha utilizado para crear muchos edificios y estructuras monumentales. Cuando se utiliza la proporción áurea en arquitectura, se dice que el edificio se crea mediante el uso de "arquitectura sagrada". Al aplicar el cálculo de la proporción áurea a un cuadrado, los arquitectos y diseñadores pueden crear el rectángulo áureo, que se cree que tiene las proporciones estéticamente más agradables para el ojo humano.
Ejemplo del Rectángulo Dorado:El Partenón

Fidias, el escultor griego, utilizó la proporción áurea en su trabajo, especialmente cuando comenzó a trabajar con las bandas que esculpió justo encima de las columnas del Partenón. También es importante señalar que el valor numérico asignado a la proporción áurea, Phi, se nombró en su honor.
Si mides las dimensiones del exterior del Partenón, descubrirás que no solo forma un Rectángulo Dorado, sino que también hay muchos Rectángulos Dorados entre las columnas. Esta estructura sagrada es un bello ejemplo de la proporción áurea en la arquitectura.
Ejemplo del Triángulo Dorado:Gran Pirámide de Giza
La Proporción Dorada, el Rectángulo Dorado y el Triángulo Dorado se pueden encontrar en la perfección de una de las Siete Maravillas del Mundo, la Gran Pirámide de Giza. Para encontrar la proporción áurea, tendrás que reducir a la mitad la base cuadrada de la pirámide y dibujar una línea vertical en el centro de la pirámide. Cuando se conecta a un lado en ángulo de la pirámide, se puede ver fácilmente cómo forma el Triángulo Dorado con una proporción de 1,618, la Proporción Dorada.
Otros ejemplos arquitectónicos
Puede encontrar muchos ejemplos de arquitectura sagrada antigua a moderna y edificios de proporción áurea.
- Catedral de Chartres - Centro, Francia
- Notre Dame - París, Francia
- Pórtico de las Doncellas - Acrópolis, Atenas
- Taj Mahal - Agra, India
- Edificio de las Naciones Unidas - Ciudad de Nueva York, Nueva York
Proporción áurea en ejemplos de arte
Puede encontrar muchos ejemplos de maestros pintores que utilizaron la proporción áurea. Estas obras de perfección fueron creadas usando la proporción de Rectángulos Dorados y Triángulos Dorados. El arte creado en base al Rectángulo Dorado demuestra ser más agradable al ojo humano. Es uno de los misterios que rodea este rectángulo perfecto y la proporción áurea.
Proporción áurea en el arte

Los ejemplos de arte de proporción áurea incluyen:
- Leonardo Di Vinci - Mona Lisa , Hombre de Vitruvio
- Botticelli - Nacimiento de Venus
- Miguel Ángel - Sagrada Familia, ' David
- Rafael - Crucifixión
- Rembrandt - Autorretrato
- Salvador Dalí - El Sacramento de la Última Cena , La persistencia de la memoria
Uso de la proporción áurea en la composición artística
Dentro de un Rectángulo Dorado hay ciertas áreas que resultan más atractivas visualmente que otras áreas. Estos puntos se descubren dibujando una línea desde la esquina inferior del rectángulo hasta la esquina opuesta y repitiéndola con la otra esquina inferior. Estas líneas se cruzarán en el centro exacto del Rectángulo Dorado. A continuación, mida la mitad de cada línea a partir del punto central. Estos cuatro puntos se llaman los ojos del rectángulo (proporción áurea). Luego se dibuja o pinta el punto focal principal de la pintura dentro de estos puntos de interés (proporciones).
Proporción áurea en la música

La música se compone de valores numéricos y cuando se utiliza la proporción áurea para crear una pieza musical, se convierte en un ejemplo vivo de las matemáticas. La secuencia de Fibonacci también prevalece en la música:
- Hay ocho notas en una escala.
- Las notas tercera y quinta son la base de los acordes.
- La longitud, u octava, de cualquier nota es de 13 notas.
La secuenciación continúa a lo largo de una pieza musical y se vuelve más compleja a medida que alcanza la proporción áurea.
Compositores que usaron la proporción áurea
Algunos de los compositores clásicos más conocidos utilizaron la proporción áurea y la secuencia de Fibonacci en sus piezas musicales, incluidos Bach, Beethoven, Chopin y Mozart. Algunos compositores modernos como Casey Mongoven han explorado la proporción áurea en su música.
Ejemplos de proporción áurea en la naturaleza

¿Dónde se encuentra la proporción áurea en la naturaleza? Está en la Espiral Dorada o Fibonacci, que se puede crear usando la Proporción Dorada. Este es un fenómeno que se encuentra ampliamente en el mundo natural. Las hojas de una planta crecen de modo que la mayor cantidad posible pueda subir en espiral por el tallo. Una nueva hoja solo se forma después de que se haya formado la anterior.
- Cactus en espiral
- Galaxias espirales
- Girasoles
Flores con la sucesión de Fibonacci
Algunas flores tienen pétalos que siguen la secuencia de Fibonacci:
- Tres pétalos: Iris, lirio, orquídeas, trillium
- Cinco pétalos: Ranúnculos, geranios, hibiscos, campanillas, capuchina
- Ocho pétalos: Delfinios
- 13 pétalos: Ciertas variedades de margaritas, hierba cana, caléndula
Espiral de Fibonacci en piñas

Dependiendo de la especie de árbol, también puede ver la proporción áurea en funcionamiento dentro de una serie de números de Fibonacci en piñas. Puedes encontrar una serie de ocho espirales en un lado de la piña, con 13 espirales en el otro. Otro patrón de piña tiene cinco espirales en un lado y ocho en el otro.
Proporción áurea en humanos
Esta proporción también es importante no solo para la forma en que los humanos se ven unos a otros, sino también para el funcionamiento de sus cuerpos y su ADN.
El ADN revela la proporción áurea
Uno de los ejemplos más sorprendentes de la proporción áurea se encuentra dentro de la estructura del ADN humano. Esto se puede ver en una sola sección transversal de ADN que revela que la doble hélice del ADN forma un decágono. Esta es una combinación de dos pentágonos, girados 36 grados entre sí, forma la doble hélice del ADN. La propia espiral de doble hélice forma un pentágono. Incluso una sola molécula de ADN revela una base de la Sección Dorada o Proporción Divina.
Las matemáticas detrás de la proporción áurea
Encontrar la proporción áurea en la vida real es simple, ya que aparece a tu alrededor. Es una perogrullada matemática que se usa para definir lo que comúnmente se conoce como el número perfecto que se encuentra en la naturaleza y que ha sido duplicado e imitado por los humanos durante siglos. La belleza simplista de este número disfraza su complejidad en la ejecución. Para comprender la teoría detrás de la proporción áurea, primero debe explorar la secuencia de Fibonacci de la proporción.
Secuencia de Fibonacci y la proporción áurea
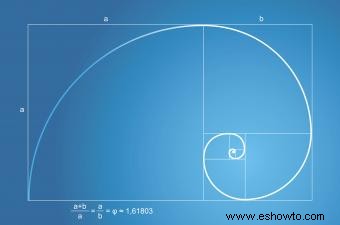
La Secuencia o Serie de Fibonacci tiene una relación con la Proporción Áurea. La serie de Fibonacci se muestra en el número de hojas de una planta y el número de pétalos de una flor. La espiral de Fibonacci, que se encuentra en la naturaleza, siempre forma parte de un rectángulo áureo con una proporción áurea.
La matemática de la serie de Fibonacci es simple:
- La secuencia comienza con 0 y 1.
- Simplemente sume los dos últimos números para obtener el siguiente número de la serie.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, etc.
- Este ejemplo de serie de Fibonacci se convierte en:1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, y así sucesivamente.
La relación de Fibonacci con la proporción áurea se realiza cuando se agrega hacia adelante, más y más. Cuanto más agregue la serie, más se acercará a la proporción áurea.
Crear un rectángulo y un triángulo áureos
Para crear un Rectángulo Dorado con la Secuencia de Fibonacci, comienzas con un cuadrado. Comenzarás a construir un rectángulo agregando otro cuadrado al cuadrado original. Recuerda usar la fórmula:0+1=1 es el primer cuadrado, 1+1=2 - agregarás otro cuadrado. 1+2=3 agregarás tres cuadrados y luego, 2+3=5, agregarás cinco cuadrados. Continuarás agregando cuadrados y eventualmente formarás un Rectángulo Dorado.
Se puede crear un Triángulo Dorado dividiendo un Rectángulo Dorado desde una esquina a la esquina opuesta. Esto crea un triángulo donde sus tres lados o ángulos tienen una proporción de 2:2:1, lo que significa que los dos lados largos tienen la misma longitud y el ángulo corto es exactamente la mitad de la longitud de los dos más largos.
Proporción áurea en el mundo real
La proporción áurea a menudo se conoce como la proporción divina debido a su importancia en la naturaleza y en los cuerpos humanos. El descubrimiento de que la proporción áurea está presente en tantos seres vivos fomentó una reverencia por esta proporción mágica, y sigue siendo una inspiración para artistas y creadores en la actualidad.

